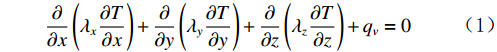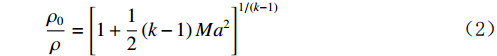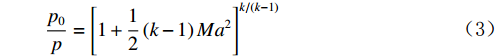Application of Numerical Simulation in Lecture of Principle of Metallurgy Transport for Material Processing
-
摘要:
结合平板传热、超音速射流特性和多相流等CFD计算案例,给出利用数值模拟仿真软件进行材料加工冶金传输原理教学的具体方法。将数值模拟仿真技术引入教学环节,既有助于学生掌握和理解教师在语言上难以表达、变化过程复杂或肉眼观察不到的传输现象,又能使学生体会自己动手模拟解决工程简化流体问题所带来的兴趣和成就感,以此提高学生学习的积极性、主动性和对所学知识的理解和应用的能力,促进学生顺利完成对材料加工冶金传输原理课程的学习,真正掌握相关动量传输、热量传输和质量传输基础理论知识。
Abstract:The current study provides a teaching method by applying numerical simulation in lecture of principle of metallurgy transport for material processing based on CFD case of plate heat transfer, supersonic jet and multiphase flow simulation. Introducing numerical simulation in lecture can not only help student understand some transport phenomena which are difficult to express, to observe or complex, but also heighten student’s interest and sense of fulfillment by solving engineering problems. This will strengthen students’ enthusiasm and initiative in learning and their ability to understand and apply the knowledge they have learned and also promotes students to successfully complete the lecture of principle of metallurgy transport for material processing so as to help them truly master the basic theoretical knowledge of momentum, heat and mass transfer.
-
Keywords:
- numerical simulation /
- transport /
- heat transfer /
- teaching
-
一. 引言
材料加工冶金传输原理是我校材料成型与控制工程专业一门十分重要的专业基础课。该课程公式多,内容抽象,学生如果对理论缺乏认识,就难以很好地理解和吸收所讲授的内容。在目前课时普遍压缩的情况下,如何通过有限学时教学使学生掌握专业所需要的传输理论基础知识,是当前我校材料加工冶金传输原理课程教学改革与建设面临的主要问题。因此,对传输原理课程教学方式方法进行认真的探索,对现行传输原理课程的教学手段等进行改革势在必行。
计算流体力学(Computational Fluid Dynamics,CFD)是流体力学和计算机科学相互融合的一门新兴交叉学科,也是数值模拟仿真的一个重要分支。目前比较著名的CFD软件包括FLUENT、COMSOL、CFX和OpenFOAM等[1-2],这些软件可以从计算方法出发,利用计算机快速的计算能力得到流体控制方程的近似解。20世纪90年代后随着计算机以及相关技术的迅猛发展,CFD得到了飞速发展,逐渐与实验流体力学一起成为独具特色的学科,成为求解传热、传质、动量传输、燃烧、多相流和化学反应等领域的复杂问题的有力工具,并广泛应用于化工、冶金、生物医药、航空航天、高铁、汽车和建筑设计等诸多工程领域。
有鉴于此,本文从材料加工冶金传输原理教学实践出发,通过将CFD软件FLUENT[3-4]引入传输原理的教学中,形象地向学生展示材料加工冶金传输原理的概念和模型,将抽象的概念、理论和复杂的数学公式变成形象的画面,并结合基础理论进行对比讲解,提高学生的学习兴趣,使学生加深对冶金和材料加工过程中的传热、传质和动量传输等知识的了解和认识,提高学生对理论的理解能力以及运用基础理论解决实际问题的能力。
二. 材料加工冶金传输原理课程的特点
材料加工冶金传输原理是一门通过数学和物理方法对复杂问题进行解析、量化和建模的学科,主要包括动量传输、热量传输和质量传输(简称“三传”)。在教学中,其教学内容既要照顾到经典动量、热量和质量传输的基本原理,又要充分反映当代“三传”最新发展,同时也要涉及冶金专业的具体应用案例。
传统的教科书中,基本概念如梯度、旋度、散度、流场、流线、温度场、浓度场和辐射强度等均是通过抽象的语言或数学公式表述,公式和概念多是材料加工冶金传输原理课程最大的特点。学生在理论学习时,对导数、微分方程等望而生畏,对于公式描述的实际现象缺乏直观了解,导致对理论不能理解或理解不到位。而由于课程的特点和要求,又不能对数学公式等进行教学上的简化,所以说,公式是学生学习这门课程无法回避的问题。
另一方面,材料加工冶金传输原理中涉及的部分数学方程,例如纳维斯-托克斯、热量守恒、湍流边界层计算、对流给热系数计算和不规则物体辐射计算等方程,是无法靠常规方法求解的,或者无法利用简单的计算器求解,只有一些个别的、简单的现象可以通过公式求解。因此,通过手动计算解决工程问题的应用场景有限。学生在学习过程中大部分情况只能看见公式,却不清楚方程在应对特定现象下的解,因而往往有这样的疑问:“既然都解不出来,学它还有什么用?”
因此,在材料加工冶金传输课程的教学过程中,使学生掌握“三传”理论知识部分虽然意义重大,但是如果一味地强调概念的理解、“三传”数学理论、公式推导及计算,学生很难从课程的大量数学推导中解脱出来,很难专注于工程实际问题的求解。课程学完后,学生不仅没有获得流体流动、传热和传质的基本知识,而且仍然不知道如何对一个具体冶金和成型方面的传输问题进行分析,从而也不可能达到学以致用的目的。课本复杂公式和实际工程中的“三传”现象,缺乏一个“可视化”衔接。对于本课程来讲,CFD软件就是一个非常有用的桥梁。利用软件对“三传”现象进行建模并求解方程,通过展示计算过程和结果进行辅助教学,可以帮助学生在掌握基础理论的同时,形象地认识到所学知识在对实际工程问题分析的重要作用,加深学生对理论的理解,提高学生对理论的应用能力。
三. 数值模拟仿真在材料加工冶金传输原理课程教学中的应用
在动量传输、热量传输和质量传输的守恒方程推导部分的教学中,选取空间某一段区域即控制体为研究对象,以基本的实验定律或经验为依据,提出假设,定义连续介质、不可压缩、理想流体、传热和传质等模型,建立起数学符号与物理量之问的联系,经过逻辑推理或严密的数学推演,形成系统的物理理论并使之数学公理化、规范化,形成牛顿粘性定律、连续性方程、边界层理论、传热和传质等知识。教师在讲授过程中,从宏观引入现象,以微观的方式讲解“三传”理论,学生整个过程中所见到的方程推导过程繁琐,很难将方程和宏观现象联系起来。部分学生即使学懂了方程,在没有应用方程解决实际问题前,很难对方程有较深的理解,更谈不上应用。数值模拟计算为课堂教学提供了一个非常好的可视化手段,可以形象地向学生展示一个从现象到建立方程,再从求解方程到解决实际问题的过程,帮助学生理解理论方程在求解实际问题的重要地位和作用,加深印象,提高应用能力。
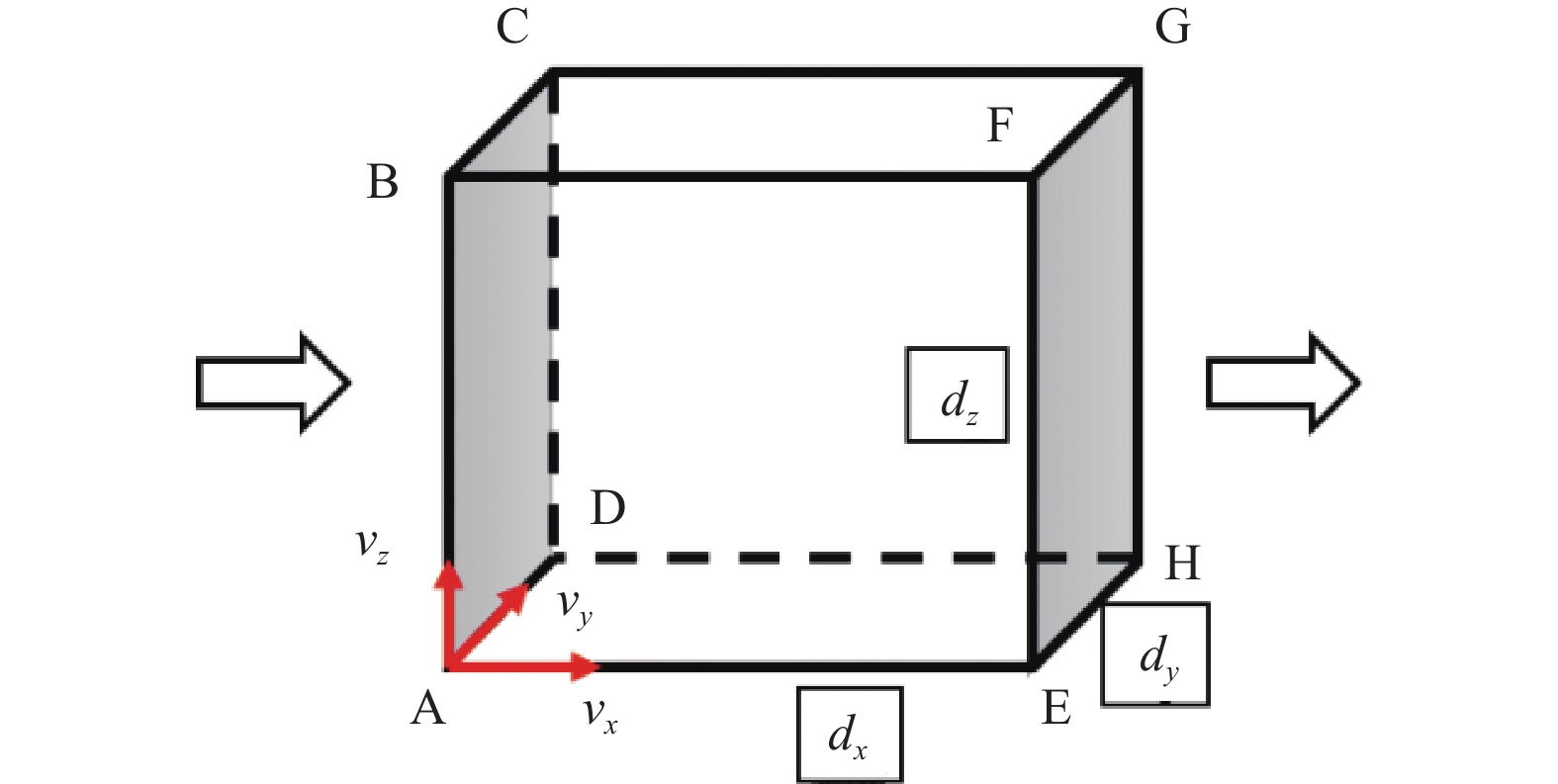
材料加工过程中涉及到铸锻件的传热问题,在分析物体的温度场时,需要建立描述物体各个点温度与空间的内在联系微分方程,或称为热量传输微分方程。在讲授方程推导时,一般采用微元体积分析法,即从固相体积中取一个如图1所示的立方体微元,其体积dv=dxdydz,分析其热量的流入和流出,根据热力学第一定律导出固体能量微分方程,如式(1)所示。
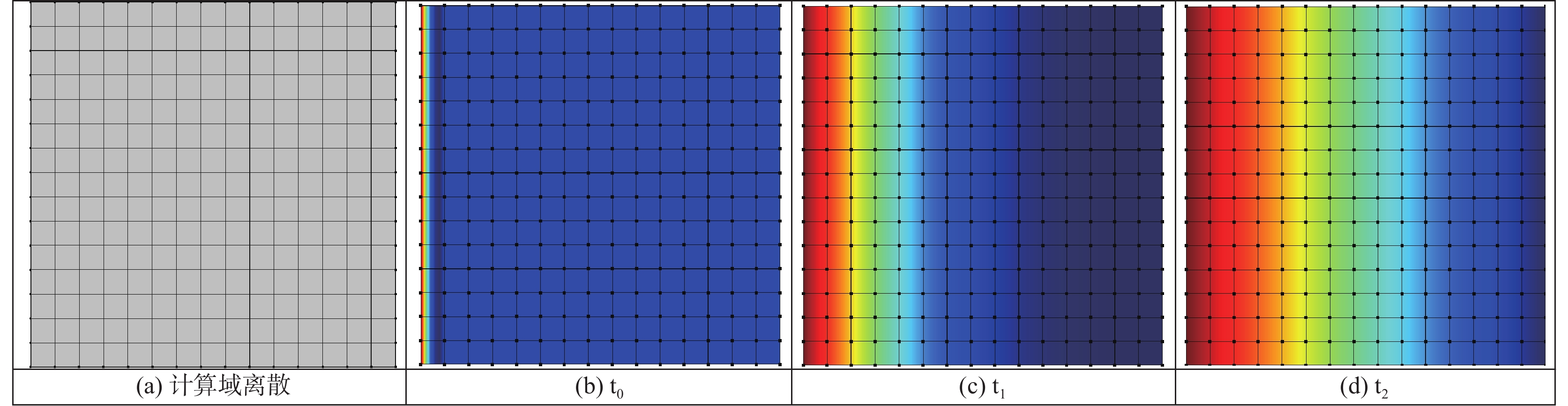
$$ \frac{\partial }{\partial x}\left({\lambda }_{x}\frac{\partial T}{\partial x}\right)+\frac{\partial }{\partial y}\left({\lambda }_{y}\frac{\partial T}{\partial y}\right)+\frac{\partial }{\partial z}\left({\lambda }_{z}\frac{\partial T}{\partial z}\right)+{q}_{v}=0 $$ (1) 其中,T为温度;λ为材料的导热系数;qv为内热源。
在利用微元体积分析法得出能量守恒方程的过程中,一方面,学生理解此体积微元为传热研究对象的一部分,另一方面,学生着眼点在体积微元上,基本能理解方程的推导过程。但是,学生很难在脑海中建立方程中描述的参数与实际物体的传热之间的关系,不能透彻地理解方程中各个参数在实际物体中的意义。因此,在讲授此部分内容时,利用计算机对一块金属板传热过程进行建模,计算金属板在加热过程中整个板的温度随时间的变化关系,如图2所示。
图2(a) 为计算域的离散,计算域被划分为若干个小的体积微元,每个微元与图1中的微元类似,每个微元与四周的体积微元通过方程1建立传热关系。假设计算域的左侧边界为热源,其它边界均为绝热。计算域的温度瞬态变化如图2(b)-(d)所示。从图中可以看出,通过方程1建立传热关系的各体积微元在同一时刻温度分布不同,在不同时刻温度也会产生变化。同时通过这个仿真结果让学生认识到:影响计算域传热效果的因素不仅有边界温度和时间,也跟物质本身性质有关,比如导热系数,这些因素在方程1中都有体现。通过这个例子的学习,让学生至少理解传热基本方程相关的三个问题:
(1)计算域的离散。理解构建微分方程过程中假设体积微元的意义,以及此种假设在构建实际物体传热方程中的作用。
(2)温度边界条件。理解实际物体传热必须有初始条件,这是求解问题的必要条件。
(3)温度变化规律。理解传热方程中的所有参数与实际传热过程的相关性,加深对传热方程的认识和应用。
通过以上的学习,建立了一个从实物到微元,通过对方程进行求解,再到实物的过程(如图3所示),形象地让学生深刻理解所学方程在解决问题中的重要作用,以及影响传热过程因素在方程中的体现,有助于学生进一步深刻领悟方程的意义,避免了学生在传统传热方程学习中“只见树木不见森林”的窘境。通过引入数值计算的结果,学生在这个过程中较快地理解了方程所要表达的内在含义,使学生在后面学习中对方程每一项所代表的含义有更深刻的认识。另外,模拟结果所展现的形象表达方式,使学生更愿意去思考方程的意义。在这个过程中,仿真模拟是理解方程和实际物体之间的一个重要且有效的纽带。
超音速射流在火箭发动机设计、3D打印和机械加工等行业具有广泛的应用,在冶金行业中,除顶吹转炉炼钢使用的氧枪外,在电炉和粉末冶金制粉行业也有应用。其基本理论学习为本课程中“可压缩气体流动”一章涉及到的气体可压缩的特性及规律。通常情况下,气体的密度随着压强和温度的变化而变化,但当气体的速度相对于当地音速很小时,其密度变化不大,可以当做不可压缩气体处理。人们在日常生活中所接触的和气体相关的大量现象,也基本可以按照不可压缩来处理。因此,当气体以接近音速或超过音速的速度运动时,其流动参数和不可压缩气体有本质上的差别,此时学生对于气体的可压缩性缺乏直观认识,很难理解可压缩气体在高速条件下的动力学规律以及气体在开放空间流动过程中各个参数的变化。虽然课程中学习了推导一维等熵流动的基本方程来认识气体的可压缩性及拉瓦尔喷管流动参数的变化规律,但是其描述公式是非线性的,学生很难想象各个参数在流动过程中的变化规律和关系。描述拉瓦尔喷管中不同截面处的密度、压力、温度和截面处马赫数关系的基本方程如式(2)—(4)。
$$ \frac{{\rho }_{0}}{\rho }={\left[1+\frac{1}{2}\left(k-1\right){Ma}^{2}\right]}^{1/\left(k-1\right)} $$ (2) $$ \frac{{p}_{0}}{p}={\left[1+\frac{1}{2}\left(k-1\right){Ma}^{2}\right]}^{k/\left(k-1\right)} $$ (3) $$ \frac{{T}_{0}}{T}=1+\frac{k-1}{2}{Ma}^{2} $$ (4) 其中,ρ0为环境密度,ρ为拉瓦管任意截面处的密度;p0为环境压力,p为拉瓦管任意截面处压力;T0为环境温度,T为拉瓦管任意截面处的温度;k为气体常数;Ma为任意截面处马赫数,其为速度与当地音速的比值。从中可以看出,使用拉瓦尔管产生超音速流动的过程中,拉瓦管任意截面处的密度、压力和温度都随着当地马赫数或速度而变化,且任意截面处的马赫数都非常数。因此,从公式上理解拉瓦管截面处各个参数的变化规律对学生来讲较为困难。
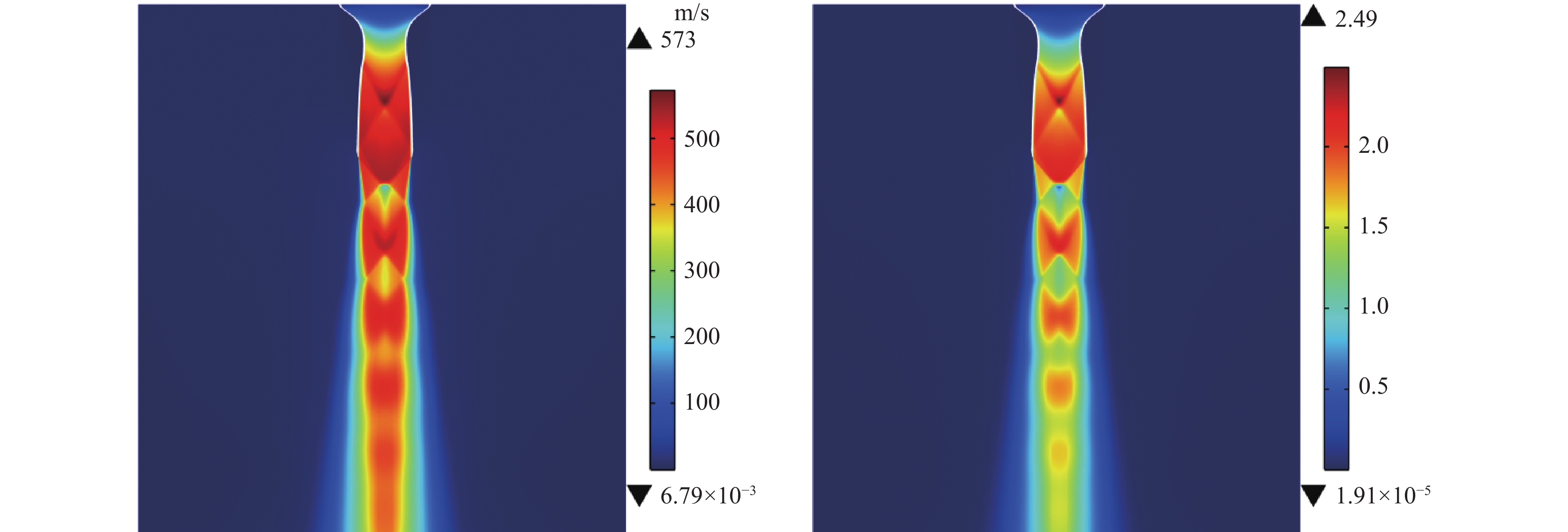
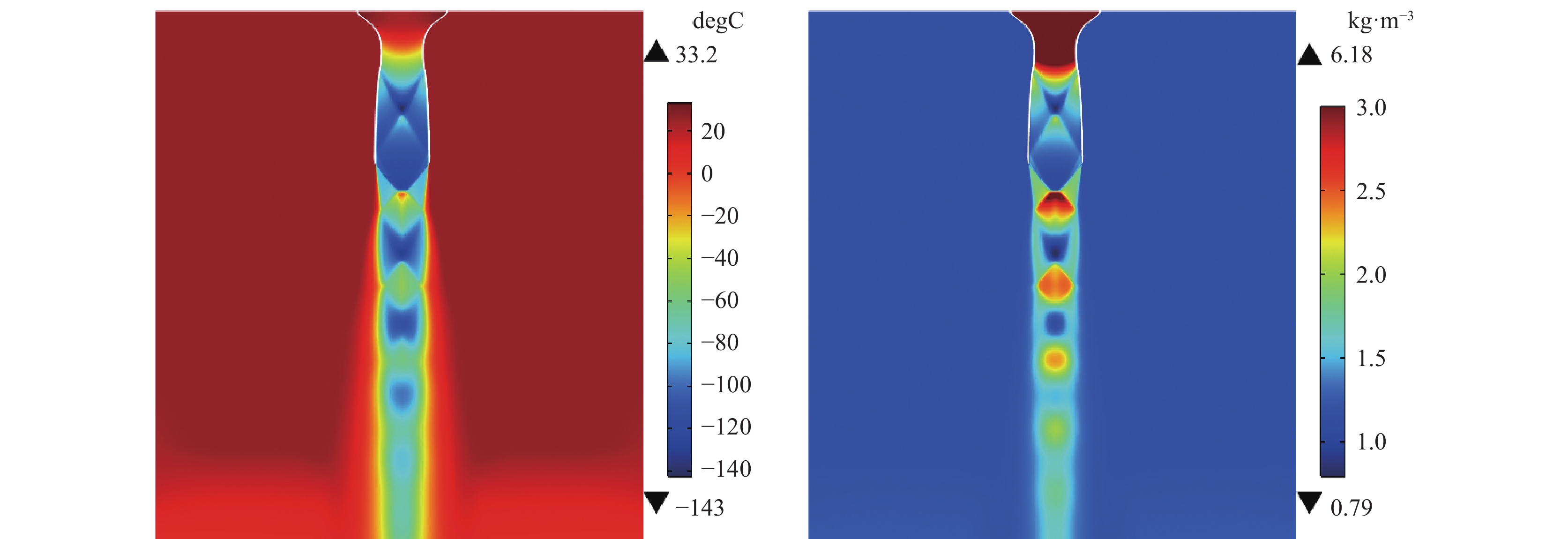
通过计算机进行建模,联立求解连续性方程、动量方程、能量方程和湍流方程对拉瓦管在工况条件下的超音速射流进行计算,射流速度场和马赫数如图4所示。从图中可以看出,气体经过拉瓦管后产生超音速射流,同时产生“马赫环”,模拟结果非常直观地展现了高压气体在经过拉瓦管后的加速过程,并展示了气体在环境中的速度和马赫数变化规律。除速度外,气体密度和温度也产生较大变化,其变化规律如图5所示。与图4中速度变化相对应,射流密度和温度都随着速度的提升而下降。图4和图5的计算结果,形象地展示了超音速射流的形成过程和重要参数在气体加速和衰减过程中的变化规律。通过模拟结果的展示,学生在学习过程中能更直接观察到超音速气流在形成过程和速度、密度、压力等参数的变化过程。可以说,数值模拟结果是方程所对应的实际世界的“再现”。与枯燥的公式学习相比,更能激发学生的学习兴趣,并使学生深刻理解公式所要表达的信息。从课堂提问过程学生的回答效果看,多数学生在学习完方程后,不能很好地描述整个超音速过程。而在方程后介绍后引入数值模拟结果并进行讲解,理解超音速过程中气流参数变化的学生数量明显增多。
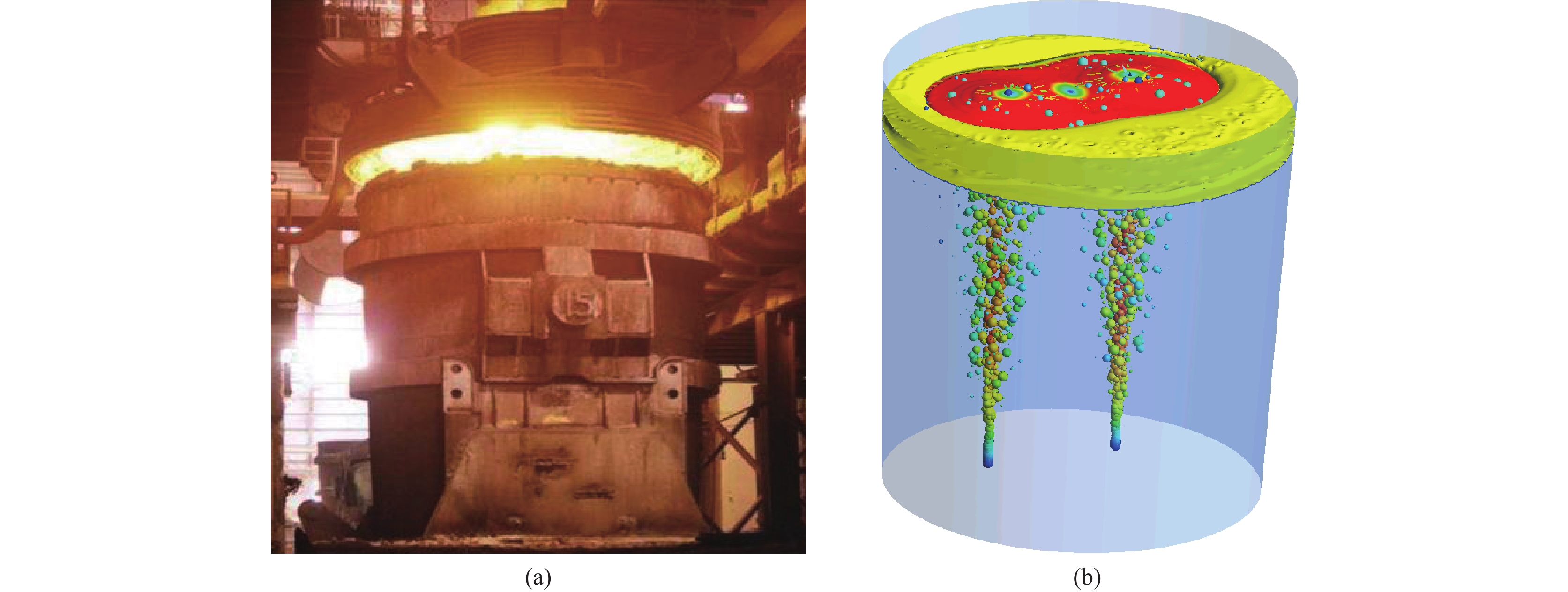
除以上的基本的“三传”现象,冶金专业还涉及到气-液、气-固、固-液和气-液-固等多相流动,相对单相流动传热问题,多相流的求解更为复杂。冶金器的主要特点是炉内为复杂的多相流,涉及钢液、渣、气流和气泡的流动、传热、气-液和液-液的相互强耦合作用。实际生产过程中,多数冶金器都在1 500℃以上的高温下操作进行,对冶金器内的钢液流动和传热等现象进行观察和测量较为困难。因此,不论是在本课程还是专业课的授课过程中,学生只通过实际生产图片,很难想象其中的钢液流动现象,更难和理论相联系,例如图6(a)钢包现场冶炼过程。通过CFD数值模拟建模并计算,能很直观形象地展示冶金传输原理中的“三传”方程在描述冶金器时的求解结果,了解到熔池在气体驱动下的流动和传热方式、气流与熔池的相互作用、渣金界面相互作用、气泡运动行为和气泡与钢液间相互作用等现象,如图6(b)所示。从图中能直观地观察到冶金器中的流动、传热、多相流和气泡分布等现象。学生能较为直观地观察并深刻理解其中现象,根据模拟结果再反向学习相关“三传”理论,能更进一步加深对理论的理解,这对于学生理解方程并建立理论和实际现象之间的联系有非常好的效果。
四. 结语
本文以具体实例展示了仿真技术在解释基本概念和复杂物理现象方面的关键作用。从中可以看出,在材料加工冶金传输原理课程教学中通过引入数值模拟仿真结果,将晦涩难懂的数学公式转化为更为直观的数据图片,不仅使学生能先入为主地理解所学知识的物理现象,更能有效建立基础理论和实际应用的桥梁,提高学生对该课程的学习兴趣,使其更好地理解和掌握该课程的重要内容。
-
[1] 杨世铭, 陶文铨. 传热学[M]. 北京: 高等教育出版社, 2006: 1-2. [2] 陶文铨. 数值传热学[M]. 西安: 西安交通大学出版社, 2001: 28-29. [3] 韩占忠, 王敬, 兰小平. FLUENT流体工程仿真计算实例与应用[M]. 北京: 北京理工大学出版社, 2004: 249-264. [4] 王福军. 计算流体动力学分析[M]. 北京: 清华大学出版社, 2004: 185-199. -
期刊类型引用(1)
1. 陈军奇,陈进武,徐道芬. “材料加工冶金传输原理”课程教学改革与实践. 科教导刊. 2025(04): 42-44 .  百度学术
百度学术
其他类型引用(0)



 下载:
下载: