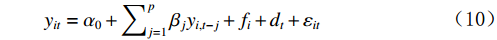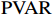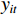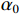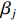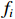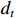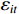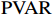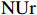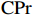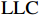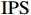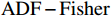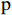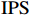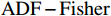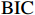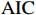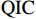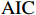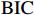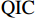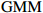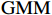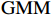A Study of the Relationship among Industrial Structure Upgrading, New Urbanization and Common Prosperity-A Case Study of Guangdong Province
-
摘要:
基于2010—2020年广东省21个地级市的数据,通过产业结构升级系数测算产业结构升级水平,运用熵值法测算新型城镇化水平及共同富裕水平,并使用PVAR模型实证分析三者的互动关系。研究结果表明:广东省产业结构升级水平、新型城镇化水平以及共同富裕水平存在空间差异;产业结构升级与新型城镇化对共同富裕的贡献较大,而共同富裕对产业结构升级、新型城镇化的贡献较小。
Abstract:Based on the data of 21 prefecture-level cities in Guangdong Province from 2010 to 2020, the entropy weight method is used to calculate the level of industrial transformation and upgrading, the level of new urbanization and the level of common prosperity, and the PVAR model is used to empirically analyze the interaction among the three. The research results show that there are spatial differences in the level of industrial transformation and upgrading, new-type urbanization and common prosperity in Guangdong Province; industrial transformation and upgrading and new-type urbanization have a greater contribution to common prosperity, while common prosperity has less contribution to industrial transformation and upgrading and new-type urbanization.
-
一. 引言
共同富裕是社会主义的本质要求。党的十九届五中全会强调把人的全面发展、全体人民共同富裕取得更为明显的实质性进展作为2035年基本实现社会主义现代化远景目标的重要内容[1]。产业结构升级是推动新型城镇化发展的重要举措,新型城镇化是实现共同富裕目标的有力支撑[2]。当前我国发展不平衡不充分问题已经比较突出,城乡收入、区域收入差距较大,因此,发挥产业结构优化升级以及新型城镇化对共同富裕目标推进的作用极其重要。
学术界关于产业结构升级与新型城镇化关系的研究主要可归纳为三个方面:产业结构升级对新型城镇化的影响、新型城镇化对产业结构升级的影响以及产业结构升级与新型城镇化的互动关系研究。在区域经济转型发展的过程中,新型城镇化与产业结构升级相互影响[3],新型城镇化发展从促进要素流动、改变市场需求、提升空间环境三方面作用于产业结构升级[4];产业结构升级在提供发展动力、改变就业结构、优化城镇功能三方面作用于城镇化[5]。产业结构升级与新型城镇化的互动并不是平衡的,熊兴等[6]的研究认为,成渝地区产业结构升级对新型城镇化的影响作用逐渐增强,新型城镇化对产业结构升级的支撑性不足。
产业结构升级通过影响居民收入差距对共同富裕产生间接的作用。三大产业发展对收入差距的影响是有差异的,从城乡收入差距看,第二产业发展会导致城乡收入差距进一步扩大,而第三产业发展则可以有效抑制城乡差距进一步扩大[7]。从区域收入差距看,中部和西部地区第三产业发展对城乡收入差距缩小的作用强于东部地区[8]。在不同时期,产业结构升级对收入差距的影响存在差异,周国富等[9]对产业结构升级、城镇化与收入差距的门槛效应分析发现:当城镇化水平处于初级阶段时,产业结构合理化和高级化扩大了城乡收入差距;当城镇化水平越过第一门槛值进入中级阶段后,产业结构合理化的影响减弱为不显著,而产业结构高级化仍在显著扩大城乡收入差距;当城镇化水平越过第二门槛值进入高级阶段后,产业结构合理化和高级化都表现为显著缩小城乡收入差距。
新型城镇化通过缩小城乡收入差距间接促进共同富裕[10]。新型城镇化与共同富裕存在着空间相关性,新型城镇化直接或间接对共同富裕各维度产生显著的促进作用,共同富裕不仅受新型城镇化的影响,还受城市初始经济发展的影响[11]。
通过文献梳理发现,对于产业结构升级与新型城镇化的研究成果较为丰富,而对于产业结构升级、新型城镇化与共同富裕的研究比较少。新型城镇化进程、产业结构升级进程会对共同富裕目标实现有着重要的影响。本文基于2010—2020年广东省21个地级市的数据,测度产业结构升级、新型城镇化与共同富裕水平,再建立
$ \mathrm{P}\mathrm{V}\mathrm{A}\mathrm{R} $ 模型研究三者之间的互动关系。二. 产业结构升级、新型城镇化与共同富裕水平测度
本文数据来源于《广东省统计年鉴》、广东省各地级市的统计年鉴,缺失数据根据各地级市的《国民经济与社会发展统计公报》的数据运用插值法进行补全。
一 模型设定
1 产业结构升级水平测度方法
本文参考徐仙英等[12]和刘建江等[13]关于产业结构升级的内涵,使用产业结构升级系数测度广东省21个地级市产业结构升级水平,具体模型如式(1)所示。
$$ \mathrm{L}=\sum \nolimits_{n=1}^{3}{l}_{s,n,t}\times i \;\;\;\;\;\;\;\;\mathrm{n}=\mathrm{1,2},3 $$ (1) 式中,
$ \mathrm{L} $ 表示产业结构升级系数,$ {l}_{s,n,t} $ 为$ \mathrm{s} $ 地区$ \mathrm{n} $ 产业在$ \mathrm{t} $ 时期的产值比重,$ \mathrm{L} $ 值介于1~3,$ \mathrm{L} $ 值越大表示产业结构升级水平越高。2 新型城镇化与共同富裕水平测度方法
使用熵值法测算广东省21个地级市新型城镇化与共同富裕的水平,熵值法确定综合得分的过程如下。
(1)无量纲化处理。采用归一化进行无量纲化处理,具体的处理过程如下:
首先建立原始数据的基本矩阵。
$$ \mathrm{N}={\left\{{\mathrm{X}}_{\mathrm{i}\mathrm{j}}\right\}}_{\mathrm{n}\times \mathrm{m}} $$ (2) 式(2)中,
$ \mathrm{n} $ 为行,$ \mathrm{m} $ 为列,$ \mathrm{i} $ 为第$ \mathrm{i} $ 行,$ \mathrm{j} $ 为第$ \mathrm{j} $ 列。对产生正向影响作用的指标,用式(3)进行处理。
$$ X_{ij} '=\frac{X_{ij}-Min\left(X_{ij}\right)}{Max\left(X_{ij}\right)-Min\left(X_{ij}\right)} $$ (3) 对产生负向影响的指标,用式(4)进行处理。
$$ X_{ij} '=\frac{Max\left(X_{ij}\right)-X_{ij}}{Max\left(X_{ij}\right)-Min\left(X_{ij}\right)} $$ (4) 式(4)中,
$ {X}_{ij} $ 是指$ \mathrm{i} $ 市第$ \mathrm{j} $ 个具体指标经过归一化处理之后所得到的数值,$ Min(X_{ij}) $ 是指标的最小值,$ Max(X_{ij}) $ 是指指标的最大值。(2)熵值法计算综合得分
计算第
$ \mathrm{j} $ 个指标下第$ \mathrm{i} $ 个样本占该指标的比重。$$ {P}_{ij}=\frac{{Z}_{ij}}{\sum _{i=1}^{m}{Z}_{ij}}(i=1,2,\cdots , m\text{;}j=\mathrm{1,2},\cdots ,n) $$ (5) 计算第
$ \mathrm{j} $ 个指标的熵值:$$ {e}_{j}=-k\sum \nolimits_{i=1}^{m}{P}_{ij}ln\left({P}_{ij}\right) $$ (6) 其中,
$ \mathrm{k} > 0 $ ,$ \mathrm{l}\mathrm{n} $ 为自然对数,$ {e}_{j} $ >0。式中$ \mathrm{k} $ 是与样本数$ \mathrm{m} $ 有关的常数,一般$ \mathrm{k}=1/\mathrm{l}\mathrm{n}\left(\mathrm{m}\right) $ ,$ 0\le {\mathrm{e}}_{\mathrm{j}}\le 1 $ 。计算第
$ \mathrm{j} $ 个指标的信息效用值。$$ {d}_{j}=1-{e}_{j} $$ (7) 计算各项指标的权重:
$$ {w}_{j}=\frac{{d}_{j}}{\sum _{i=1}^{n}{d}_{j}} $$ (8) 计算各样本的综合得分:
$$ {s}_{i}=\sum \nolimits_{j=1}^{n}{w}_{j}\times {p}_{ij}(i=\mathrm{1,2},\cdots ,m) $$ (9) 二 变量指标体系概况
新型城镇化区别于传统城镇化,新型城镇化把生态文明理念和原则全面融合到城镇化的全过程,走集约化、智能、绿色、低碳的新型城镇化道路[13]。本文借鉴李伟军等[14]、熊兴等[6]的做法,采用综合指标法,选取了人均GDP、第三产业产值比重、人均地方财政收入等11个指标,构建了测度新型城镇化水平的指标体系。共同富裕具有鲜明的时代特征和中国特色,是全体人民通过辛勤劳动和相互帮助,普遍达到生活富裕富足、精神自信自强、环境宜居宜业、社会和谐和睦、公共服务普及普惠,实现人的全面发展和社会全面进步,共享改革发展成果和幸福美好生活[15]。本文基于数据的可获得性,借鉴陈丽君等[16]、孙学涛等[11]的做法,从富裕程度、城乡差距和区域差异三个层面,选取了14个指标,构建共同富裕的指标体系。产业结构升级的内涵可概括为产业结构高级化、资源配置方式市场化、产业发展方式集约化、产业空间结构的集聚以及微观层面上产业内企业与产品结构的升级[13]。本文使用产业结构升级系数测度广东省21个地级市产业结构升级水平。具体指标体系如表1所示。
表 1 变量指标体系一级
指标二级指标 三级指标 基础指标 指向性 新型城镇化 发展水平 经济发展 人均$ \mathrm{G}\mathrm{D}\mathrm{P} $ + 第三产业产值比重 + 人均地方财政收入 + 社会发展 每万人拥有医院床位数 + 人均社会消费品零售总额 + 发展效率 生态效率 人均公园绿地面积 + 单位$ \mathrm{G}\mathrm{D}\mathrm{P} $电耗 − 单位$ \mathrm{G}\mathrm{D}\mathrm{P} $能耗 − 城乡协调 城乡经济
差距城乡居民收入比 − 城乡居民消费比 − 城镇化水平 城镇化率 + 共同
富裕富裕程度 城镇收入 城镇居民人均可支配收入 + 农村收入 农村居民人均可支配收入 + 城镇消费
支出城镇居民人均消费支出 + 农村消费
支出农村居民人均消费支出 + 居民消费
水平人均社会零售品总额 + 城乡差距 城乡收入
协调城乡居民收入比 − 城乡消费
协调城乡居民消费支出比 − 区域差距 城镇化水平 常住人口城镇化率 + 区域间收入
差距城市居民人均可支配收入与广东省居民人均可支配收入之比 + 农村居民人均可支配收入与广东省农村居民人均可支配收入之比 + 区域间消费
差距城市居民人均消费支出与广东省城镇居民人均消费支出之比 + 农村居民人均消费支出与广东省农村居民人均消费支出之比 + 区域医疗
差距万人医院床位数与广东省每万人医院床位数之比 + 区域公共基
础设施差距人均公园绿地面积与广东省人均公园绿地面积之比 + 产业结构升级 产业结构升级系数 三 测算结果及分析
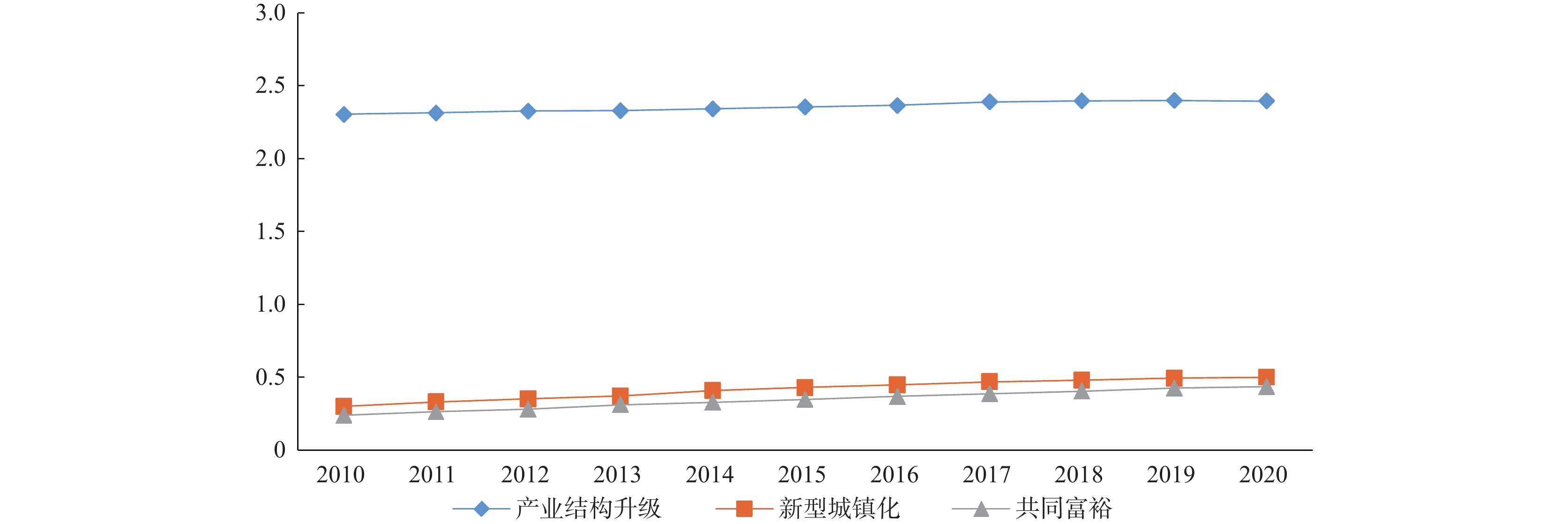
根据表1所选指标体系,结合产业结构升级系数计算出产业结构升级水平、熵值法计算新型城镇化水平和共同富裕水平,各测算结果如表2所示。
表 2 产业结构升级水平、新型城镇化水平与共同富裕水平测度结果城市 产业结构升级水平 新型城镇化水平 共同富裕水平 2010年 2015年 2020年 2010年 2015年 2020年 2010年 2015年 2020年 广州 2.593 2.659 2.713 0.527 0.688 0.806 0.682 0.758 0.869 深圳 2.527 2.587 2.620 0.588 0.737 0.751 0.511 0.546 0.678 珠海 2.399 2.459 2.532 0.404 0.589 0.659 0.369 0.515 0.658 汕头 2.332 2.382 2.433 0.386 0.512 0.593 0.389 0.506 0.615 佛山 2.336 2.361 2.406 0.386 0.512 0.565 0.348 0.489 0.601 韶关 2.348 2.384 2.363 0.250 0.424 0.515 0.308 0.482 0.585 河源 2.301 2.361 2.412 0.236 0.412 0.515 0.177 0.347 0.461 梅州 2.231 2.311 2.290 0.408 0.517 0.509 0.214 0.308 0.387 惠州 2.183 2.241 2.393 0.320 0.429 0.479 0.192 0.306 0.385 汕尾 2.292 2.354 2.353 0.204 0.324 0.478 0.178 0.269 0.353 东莞 2.209 2.232 2.456 0.314 0.379 0.463 0.189 0.279 0.344 中山 2.483 2.528 2.460 0.287 0.347 0.460 0.165 0.245 0.338 江门 2.365 2.415 2.414 0.266 0.394 0.449 0.129 0.270 0.337 阳江 2.296 2.360 2.256 0.299 0.432 0.435 0.179 0.250 0.333 湛江 2.137 2.220 2.259 0.177 0.411 0.432 0.144 0.253 0.326 茂名 2.177 2.236 2.289 0.209 0.314 0.432 0.155 0.274 0.325 肇庆 2.236 2.274 2.232 0.231 0.323 0.422 0.149 0.249 0.321 清远 2.229 2.205 2.334 0.232 0.342 0.414 0.126 0.246 0.321 潮州 2.213 2.319 2.333 0.223 0.357 0.414 0.156 0.228 0.314 揭阳 2.303 2.327 2.437 0.219 0.333 0.408 0.123 0.255 0.314 云浮 2.207 2.227 2.303 0.160 0.275 0.340 0.149 0.239 0.304 从表2、图1可以看出,2010—2020年广东省21个地级市产业结构升级水平、新型城镇化水平以及共同富裕水平均呈现平稳上升的趋势。从新型城镇化水平来看,广州市的上升幅度最大,2010—2020年综合得分提高了0.279。从共同富裕水平来看,不同地级市共同富裕水平存在差距,2020年得分最高的广州市为0.869;其次是深圳市、珠海市、汕头市和佛山市,分别为0.678、0.658、0.615、0.601;综合得分最低的云浮市为0.304。受到地理位置和经济发展水平的影响,不同地级市的非均衡经济发展必然导致城镇化发展的差距。而共同富裕水平的高低受到新型城镇化水平以及产业结构升级水平的影响,故而共同富裕水平的变化与新型城镇化与产业结构升级的变化呈现相同的趋势[17]。
三. 产业结构升级、新型城镇化与共同富裕的实证分析
本文使用向量自回归模型(
$ \mathrm{P}\mathrm{V}\mathrm{A}\mathrm{R} $ 模型)分析产业结构升级、新型城镇化以及共同富裕三者之间的互动关系,构建的研究模型如下:$$ {y}_{it}={\alpha }_{0}+\sum\nolimits _{j=1}^{p}{\beta }_{j}{y}_{i,t-j}+{f}_{i}+{d}_{t}+{\varepsilon }_{it} $$ (10) 在
$ \mathrm{P}\mathrm{V}\mathrm{A}\mathrm{R} $ 模型中,$ {y}_{it} $ 是包含了产业结构升级、新型城镇化以及共同富裕综合得分的列变量,$ \mathrm{i} $ 表示广东省内的不同地级市,$ \mathrm{t} $ 表示不同年份,$ \mathrm{p} $ 表示滞后项,$ {\alpha }_{0} $ 为截距项向量,$ \beta_j $ 为滞后变量的参数矩阵;$ f_i $ 和$ d_t $ 分别为个体效应和时间效应,$ {\varepsilon }_{it} $ 为随机误差项。一 平稳性检验及滞后阶数的确定
1 平稳性检验
在建立
$ \mathrm{P}\mathrm{V}\mathrm{A}\mathrm{R} $ 模型之前,首先对广东省21个地级市的产业结构升级($ \mathrm{S}\mathrm{U}\mathrm{P}\mathrm{r} $ )、新型城镇化($ \mathrm{N}\mathrm{U}\mathrm{r} $ )以及共同富裕($ \mathrm{C}\mathrm{P}\mathrm{r} $ )三组变量数据进行面板单位根检验,检验三组变量是否平稳。本文采用$ \mathrm{L}\mathrm{L}\mathrm{C} $ 、$ \mathrm{I}\mathrm{P}\mathrm{S} $ 以及$ \mathrm{A}\mathrm{D}\mathrm{F}-\mathrm{F}\mathrm{i}\mathrm{s}\mathrm{h}\mathrm{e}\mathrm{r} $ 法进行检验,检验结果(括号内为$ \mathrm{p} $ 值,括号外为统计数据)如表3所示。表 3 单位根检验结果变量 检验方法 是否平稳 $ \mathrm{L}\mathrm{L}\mathrm{C} $ $ \mathrm{I}\mathrm{P}\mathrm{S} $ $ \mathrm{A}\mathrm{D}\mathrm{F}-\mathrm{F}\mathrm{i}\mathrm{s}\mathrm{h}\mathrm{e}\mathrm{r} $ $ \mathrm{S}\mathrm{U}\mathrm{P}\mathrm{r} $ 86.2500 ***
(0.0000 )− 5.4245 ***
(0.0000 )86.2500 ***
(0.0000 )平稳 $ \mathrm{N}\mathrm{U}\mathrm{r} $ 65.3799 ***
(0.0000 )− 4.0319 ***
(0.0000 )65.3799 ***
(0.0000 )平稳 $ \mathrm{C}\mathrm{P}\mathrm{r} $ 66.3441 ***
(0.0000 )− 4.4017 ***
(0.0000 )66.3441 ***
(0.0000 )平稳 所有变量在1%的显著性水平下同时通过了
$ \mathrm{L}\mathrm{L}\mathrm{C} $ 、$ \mathrm{I}\mathrm{P}\mathrm{S} $ 以及$ \mathrm{A}\mathrm{D}\mathrm{F}-\mathrm{F}\mathrm{i}\mathrm{s}\mathrm{h}\mathrm{e}\mathrm{r} $ 三种检验,这说明三个变量都是拒绝原假设,变量都是平稳的。2 滞后阶数选择
本文通过对
$ \mathrm{B}\mathrm{I}\mathrm{C} $ 、$ \mathrm{A}\mathrm{I}\mathrm{C} $ 和$ \mathrm{Q}\mathrm{I}\mathrm{C} $ 统计量最小原则来共同决定最优滞后阶数,统计结果如表4所示。根据统计量最小原则,$ \mathrm{A}\mathrm{I}\mathrm{C} $ 支持3为最优滞后阶数,$ \mathrm{B}\mathrm{I}\mathrm{C} $ 和$ \mathrm{Q}\mathrm{I}\mathrm{C} $ 均支持1为最优滞后阶数,故本文最终确定滞后阶数为1。表 4 最优滞后项的确定滞后阶数$ \mathrm{l}\mathrm{a}\mathrm{g} $ $ \mathrm{B}\mathrm{I}\mathrm{C} $ $ \mathrm{A}\mathrm{I}\mathrm{C} $ $ \mathrm{Q}\mathrm{I}\mathrm{C} $ 1 − 45.3127 *40.29036 5.570183 *2 − 18.25888 38.80983 15.66304 3 − 7.398458 21.1359 *9.562505 注:带*的数据所对应的是最优滞后阶数。 二 格兰杰因果检验
使用格兰杰因果检验来判断变量之间的格兰杰因果关系,对后文的脉冲响应分析及方差分解具有意义。本文产业结构升级、新型城镇化以及共同富裕的格兰杰因果检验如表5所示。
表 5 格兰杰因果检验表原假设(前一序列不是后一序列
的格兰杰原因)$ {Ch}^{2} $ $ \mathrm{d}\mathrm{f} $ 是否拒绝
原假设$ \mathrm{N}\mathrm{U}\mathrm{r}-\mathrm{S}\mathrm{U}\mathrm{P}\mathrm{r} $ 18.269 1 是*** $ \mathrm{C}\mathrm{P}\mathrm{r}-\mathrm{S}\mathrm{U}\mathrm{P}\mathrm{r} $ 18.730 1 是*** $ \mathrm{N}\mathrm{U}\mathrm{r}\mathrm{和}\mathrm{C}\mathrm{P}\mathrm{r}-\mathrm{S}\mathrm{U}\mathrm{P}\mathrm{r} $ 20.632 2 是*** $ \mathrm{S}\mathrm{U}\mathrm{P}\mathrm{r}-\mathrm{N}\mathrm{U}\mathrm{r} $ 19.209 1 是*** $ \mathrm{C}\mathrm{P}\mathrm{r}-\mathrm{N}\mathrm{U}\mathrm{r} $ 8.173 1 是*** $ \mathrm{S}\mathrm{U}\mathrm{P}\mathrm{r}\mathrm{和}\mathrm{C}\mathrm{P}\mathrm{r}-\mathrm{N}\mathrm{U}\mathrm{r} $ 26.489 2 是*** $ \mathrm{S}\mathrm{U}\mathrm{P}\mathrm{r}-\mathrm{C}\mathrm{P}\mathrm{r} $ 19.712 1 是*** $ \mathrm{N}\mathrm{U}\mathrm{r}-\mathrm{C}\mathrm{P}\mathrm{r} $ 10.340 1 是*** $ \mathrm{S}\mathrm{U}\mathrm{P}\mathrm{r}\mathrm{和}\mathrm{N}\mathrm{U}\mathrm{r}-\mathrm{C}\mathrm{P}\mathrm{r} $ 60.103 2 是*** 由表5可以看出,各个城市的产业结构升级、新型城镇化以及共同富裕互为格兰杰原因。新型城镇化与共同富裕同时作用于产业结构升级;产业结构升级与新型城镇化同时影响了共同富裕水平;产业结构升级与共同富裕共同作用会对新型城镇化进程产生影响。综合来看,对于广东省21个地级市而言,产业结构升级、新型城镇化以及共同富裕是相互影响的。
三 脉冲响应
在进行方差分解分析和脉冲响应分析之前,需先对PVAR模型的稳定性进行检验。其中特征值稳定性检验如图2所示。
由图2可以看出,
$ \mathrm{P}\mathrm{V}\mathrm{A}\mathrm{R} $ 模型中,所有特征值都在单位圆内,说明本文所构建的$ \mathrm{P}\mathrm{V}\mathrm{A}\mathrm{R} $ 模型是稳定的,可以进行下一步的脉冲响应分析和方差分析。1
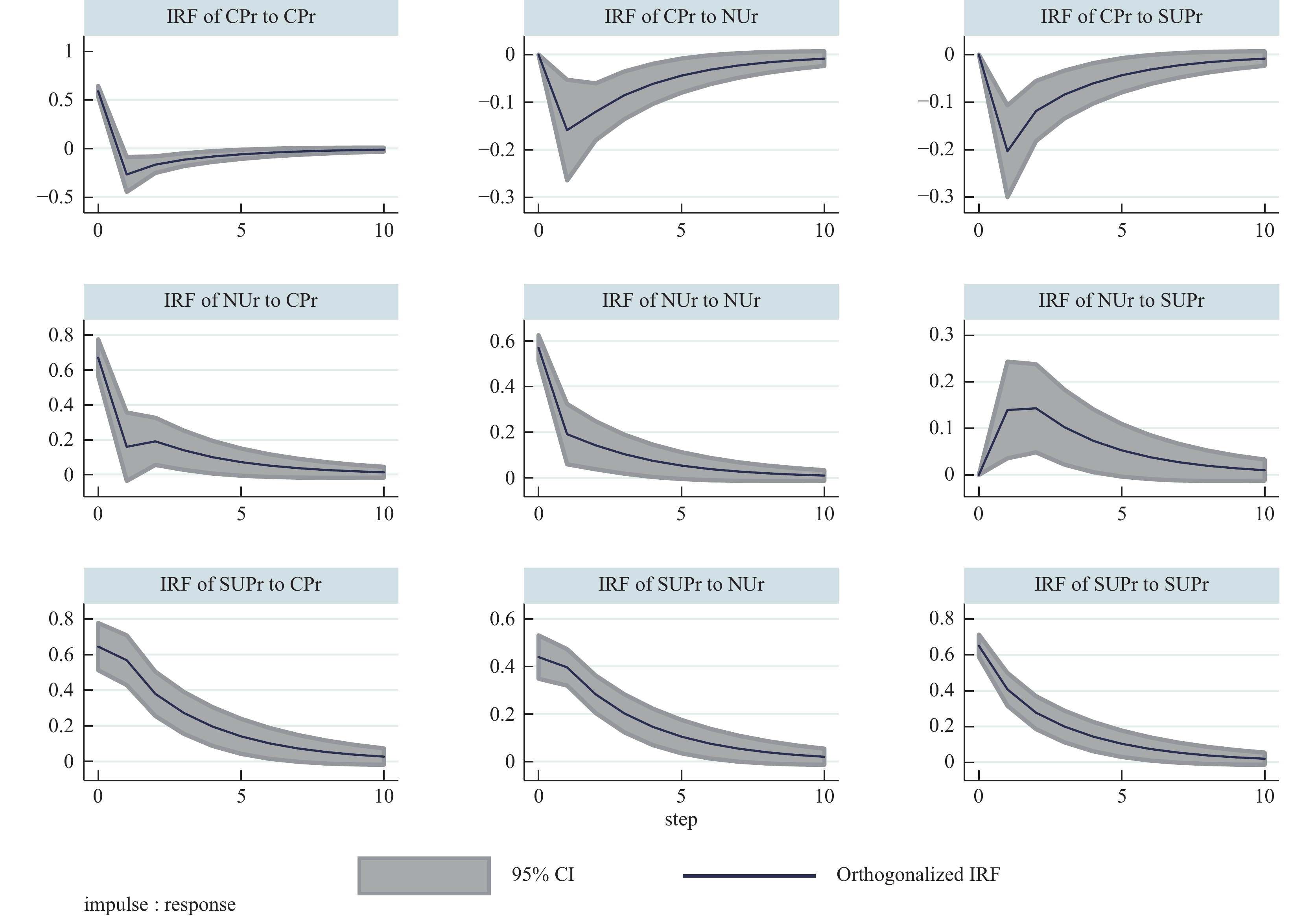
$ \mathrm{G}\mathrm{M}\mathrm{M} $ 估计在确定最优滞后阶数为1阶后,对
$ \mathrm{P}\mathrm{V}\mathrm{A}\mathrm{R} $ 模型做了$ \mathrm{G}\mathrm{M}\mathrm{M} $ 估计,$ \mathrm{G}\mathrm{M}\mathrm{M} $ 估计结果如表6所示。表 6$ \mathrm{G}\mathrm{M}\mathrm{M} $ 估计结果$ \mathrm{S}\mathrm{U}\mathrm{P}\mathrm{r} $ $ \mathrm{N}\mathrm{U}\mathrm{r} $ $ \mathrm{C}\mathrm{P}\mathrm{r} $ 滞后一期的$ \mathrm{S}\mathrm{U}\mathrm{P}\mathrm{r} $ 0.527562 ***
(4.62)0.4348363 ***
(3.96)0.7717781 ***
(4.23)滞后一期的$ \mathrm{N}\mathrm{U}\mathrm{r} $ 0.6514911 ***
(3.78)0.6539842 ***
(4.98)0.8152604 ***
(4.64)滞后一期的$ \mathrm{C}\mathrm{P}\mathrm{r} $ − 0.1347383 ***
(−4.42)− 0.2698053 ***
(−4.53)− 0.4532845 ***
(−5.39)将产业结构升级作为被解释变量时,滞后1期的产业结构升级对自身的动态影响为0.53,且在1%的水平下显著,说明广东省前期产业结构升级对后期产业结构升级具有促进作用。滞后一期的新型城镇化对产业结构升级的动态影响为0.65,且在1%的水平下显著,说明新型城镇化促进了产业结构升级。
滞后一期的共同富裕对产业结构升级的动态影响显著为负,这说明了近年来广东省共同富裕水平仍未达到理想水平,对产业结构升级的贡献较低。
将新型城镇化作为被解释变量,新型城镇化对自身的动态影响为0.65,滞后一期的产业结构升级对新型城镇化的动态影响为0.43,且均在1%的水平下显著,说明广东省前期新型城镇化对后期新型城镇化水平的提高具有促进作用;产业结构升级促进了新型城镇化水平的提高。共同富裕对新型城镇化的动态影响显著为负,说明共同富裕对新型城镇化的贡献较低。
将共同富裕作为被解释变量,产业结构升级和新型城镇化对共同富裕的动态影响均显著为正,说明产业结构升级与新型城镇化水平的提高都对共同富裕的目标具有正向作用。产业结构升级是高质量发展的重要内容,高质量发展有利于共同富裕目标的实现,因而产业结构升级对共同富裕具有间接的促进作用。新型城镇化作为要素再分配的重要过程,促进了要素在城乡和区域间的自由流动,缩小了城乡和区域差距,为实现共同富裕提供了前提条件[18]。
2 方差分解分析
由前面分析可知,最优滞后项为1期。为了进一步分析广东省产业结构升级、新型城镇化与共同富裕互动关系的可持续性,本文在滞后一期的情况下运用正交脉冲响应函数,通过200次蒙特卡罗模拟,期数为10,得到产业结构升级、新型城镇化与共同富裕变动后的脉冲响应图(图3)。图中纵轴表示冲击的程度,横轴表示冲击的滞后期数。
图3中,脉冲响应函数随着滞后期数的增加最后均趋近于0,这说明本文构建的PVAR模型是稳定的。
从脉冲响应图像的第1列可以看出:(1)当共同富裕受到自身冲击时,其对自身的影响在2期之前为正,随后转为负,并逐渐趋近于零,表明短期内,共同富裕水平对自身具有促进作用。(2)共同富裕受到新型城镇化冲击时,当期新型城镇化对共同富裕影响为正,达到
0.6150 ,这种影响从当期开始逐渐减弱,不断趋近于0。(3)当共同富裕受到产业结构升级冲击时,当期产业结构升级对共同富裕的影响为正,达到0.7010 ,这种影响从当期开始逐渐下降,不断趋近于0。说明新型城镇化和产业结构升级均对共同富裕具有正向影响,这种影响具有滞后性,并在后期趋近于0,说明新型城镇化水平提高、产业结构升级促进了共同富裕。从脉冲响应图像第2列可以看出:(1)当新型城镇化受到共同富裕冲击时,会产生持续的负向影响,并在后期趋近于0。(2)当新型城镇化受到自身冲击时,其对自身影响在当期达到最大值,为
0.6000 ,这种影响从当期开始逐渐减弱,并趋近于0,说明新型城镇化对自身影响具有长期效应。(3)当新型城镇化受到产业结构升级冲击时,这种影响在当期达到最大值0.5100 ,并从当期开始逐渐减弱,并趋近于0,说明产业结构升级推动了新型城镇化水平的提高。从脉冲响应图像第3列可以看出:(1)产业结构升级受到共同富裕冲击时,会产生持续的负向影响,并在后期趋近于0。(2)产业结构升级受到新型城镇化影响时,从当期开始这种影响逐渐增强,并在第2期达到最大值,为
0.2000 ,并从第3期开始逐渐减弱,并趋近于0。说明在短期内,新型城镇化对产业结构升级的冲击具有滞后性。(3)产业结构升级受到自身冲击时,其对自身影响在当期最大为0.6100 ,这种影响从当期滞后开始减弱,并不断趋近于0。说明短期内,产业结构升级对自身具有促进作用,这种影响在长期会趋于稳定。四. 结论与政策建议
一 结论
本文首先用产业结构升级系数计算了产业结构升级水平,使用熵值法计算了新型城镇化水平、共同富裕水平,其次利用面板向量自回归模型,基于2010—2020年广东省21个地级市的面板数据,实证分析了广东省产业结构升级、新型城镇化、共同富裕的关系,得出以下结论:
2010—2020年广东省产业结构升级水平、新型城镇化水平、共同富裕水平呈现上升趋势。但存在空间差异,广州市、深圳市、佛山市、东莞市、中山市产业结构升级水平、新型城镇化水平和共同富裕水平较高,而云浮市、湛江市、梅州市、清远市产业结构升级水平、新型城镇化水平和共同富裕水平较低。
广东省产业结构升级与新型城镇化之间相互促进。从格兰杰检验结果来看,产业结构升级与新型城镇化互为彼此的格兰杰原因;从
$ \mathrm{G}\mathrm{M}\mathrm{M} $ 估计结果来看,产业结构升级对新型城镇化的系数为正,同时新型城镇化对产业结构升级的系数也为正,说明二者之间的相互影响都是正向的;从脉冲响应分析来看,产业结构升级与新型城镇化受到彼此的冲击之后,这种影响都是正向的。由此可见,产业结构升级为新型城镇化水平提高提供了物质基础,新型城镇化发展为产业结构升级提供了基础设施的支撑。广东省产业结构升级、新型城镇化对共同富裕具有正向促进作用,而共同富裕对产业结构升级、新型城镇化的贡献较低。产业结构升级为共同富裕的实现奠定了物质基础,新型城镇化为共同富裕的实现提供了新路径。从
$ \mathrm{G}\mathrm{M}\mathrm{M} $ 估计结果来看,共同富裕对产业结构升级、新型城镇化的影响均显著为负,且系数较小,分别为-0.13和-0.27,远小于新型城镇化、产业结构升级对共同富裕的影响,系数分别为0.86和0.77。二 建议
1 在产业结构升级和新型城镇化建设进程中注重缩小空间差距
本文实证结果表明广东省产业结构升级水平、新型城镇化水平、共同富裕水平存在较大的空间差距,这对于区域发展是不利的。因而广东省在产业结构升级、新型城镇化建设过程中要根据不同规模和经济发展水平的城市的实际情况合理规划,同时注重缩小区域差距。一是推进以人为核心的新型城镇化,逐步取消城市落户限制,同时加大对湛江、韶关、清远等经济相对落后城市的基础设施建设投入,缩小其与经济发达城市公共基础设施的差距;二是逐步建成现代化城市体系,发挥广州、深圳等大城市对周边城市的空间溢出效应,间接拉动其他城市的新型城镇化水平;三是通过将珠三角地区及海内外产业和先进技术引进粤东、粤西和山区,促进产业结构升级,缩小粤东、粤西和山区与珠三角地区的发展差距。
2 因地制宜推进产业结构升级
广东省政府应当有针对性地根据区域特色出台相应的激励政策。本文实证结果表明,产业结构升级对于新型城镇化水平的提高和共同富裕有促进作用。推动产业结构升级,明确产业结构升级方向,重视稳速增质,根据不同城市的资源禀赋和自身条件,采取差异化的产业结构升级措施[19]。对于佛山、东莞、惠州等主要由工业主导的城市,产业结构升级过程中应当朝着再工业化的方向去发展;对于深圳、广州等第三产业比重较大的城市,应当进行三产化,推动产业结构向第三产业主导转型;对于清远、韶关等山区城市,应当发挥山区县域和资源优势,整合县域资源,构建山区特色现代化产业体系。
3 发挥新型城镇化与产业结构升级的相互促进作用,推动共同富裕目标实现
注重产业与城市协同发展,实现城市功能体系与产业结构互促共进、融合发展的产城融合协调发展新局面。一是推动产业结构升级,促进新型城镇化水平提高。依托广州市、深圳市的产业布局,辐射周边城市,消除区域发展不平衡问题;各地级市因地制宜制定产业发展规划,定位优势产业和支柱性产业,调整产业链,以此来促进经济发展,为新型城镇化建设提供物质基础。二是加快新型城镇化建设,推动产业结构升级。广东省新型城镇化建设应当综合考量人口、社会、经济、环境等多方面因素,合理规划城镇化发展,促进产业结构升级;新型城镇化建设过程中要注重完善社会保障体系、医疗、教育等基础设施建设,健全城乡一体化改革,实现公共基础设施一体化,对剩余劳动力进行职业教育,一方面解决人口就业问题,增加居民收入,另一方面提高劳动力素质,助力产业结构升级。
-
表 1 变量指标体系
一级
指标二级指标 三级指标 基础指标 指向性 新型城镇化 发展水平 经济发展 人均$ \mathrm{G}\mathrm{D}\mathrm{P} $ + 第三产业产值比重 + 人均地方财政收入 + 社会发展 每万人拥有医院床位数 + 人均社会消费品零售总额 + 发展效率 生态效率 人均公园绿地面积 + 单位$ \mathrm{G}\mathrm{D}\mathrm{P} $电耗 − 单位$ \mathrm{G}\mathrm{D}\mathrm{P} $能耗 − 城乡协调 城乡经济
差距城乡居民收入比 − 城乡居民消费比 − 城镇化水平 城镇化率 + 共同
富裕富裕程度 城镇收入 城镇居民人均可支配收入 + 农村收入 农村居民人均可支配收入 + 城镇消费
支出城镇居民人均消费支出 + 农村消费
支出农村居民人均消费支出 + 居民消费
水平人均社会零售品总额 + 城乡差距 城乡收入
协调城乡居民收入比 − 城乡消费
协调城乡居民消费支出比 − 区域差距 城镇化水平 常住人口城镇化率 + 区域间收入
差距城市居民人均可支配收入与广东省居民人均可支配收入之比 + 农村居民人均可支配收入与广东省农村居民人均可支配收入之比 + 区域间消费
差距城市居民人均消费支出与广东省城镇居民人均消费支出之比 + 农村居民人均消费支出与广东省农村居民人均消费支出之比 + 区域医疗
差距万人医院床位数与广东省每万人医院床位数之比 + 区域公共基
础设施差距人均公园绿地面积与广东省人均公园绿地面积之比 + 产业结构升级 产业结构升级系数 表 2 产业结构升级水平、新型城镇化水平与共同富裕水平测度结果
城市 产业结构升级水平 新型城镇化水平 共同富裕水平 2010年 2015年 2020年 2010年 2015年 2020年 2010年 2015年 2020年 广州 2.593 2.659 2.713 0.527 0.688 0.806 0.682 0.758 0.869 深圳 2.527 2.587 2.620 0.588 0.737 0.751 0.511 0.546 0.678 珠海 2.399 2.459 2.532 0.404 0.589 0.659 0.369 0.515 0.658 汕头 2.332 2.382 2.433 0.386 0.512 0.593 0.389 0.506 0.615 佛山 2.336 2.361 2.406 0.386 0.512 0.565 0.348 0.489 0.601 韶关 2.348 2.384 2.363 0.250 0.424 0.515 0.308 0.482 0.585 河源 2.301 2.361 2.412 0.236 0.412 0.515 0.177 0.347 0.461 梅州 2.231 2.311 2.290 0.408 0.517 0.509 0.214 0.308 0.387 惠州 2.183 2.241 2.393 0.320 0.429 0.479 0.192 0.306 0.385 汕尾 2.292 2.354 2.353 0.204 0.324 0.478 0.178 0.269 0.353 东莞 2.209 2.232 2.456 0.314 0.379 0.463 0.189 0.279 0.344 中山 2.483 2.528 2.460 0.287 0.347 0.460 0.165 0.245 0.338 江门 2.365 2.415 2.414 0.266 0.394 0.449 0.129 0.270 0.337 阳江 2.296 2.360 2.256 0.299 0.432 0.435 0.179 0.250 0.333 湛江 2.137 2.220 2.259 0.177 0.411 0.432 0.144 0.253 0.326 茂名 2.177 2.236 2.289 0.209 0.314 0.432 0.155 0.274 0.325 肇庆 2.236 2.274 2.232 0.231 0.323 0.422 0.149 0.249 0.321 清远 2.229 2.205 2.334 0.232 0.342 0.414 0.126 0.246 0.321 潮州 2.213 2.319 2.333 0.223 0.357 0.414 0.156 0.228 0.314 揭阳 2.303 2.327 2.437 0.219 0.333 0.408 0.123 0.255 0.314 云浮 2.207 2.227 2.303 0.160 0.275 0.340 0.149 0.239 0.304 表 3 单位根检验结果
变量 检验方法 是否平稳 $ \mathrm{L}\mathrm{L}\mathrm{C} $ $ \mathrm{I}\mathrm{P}\mathrm{S} $ $ \mathrm{A}\mathrm{D}\mathrm{F}-\mathrm{F}\mathrm{i}\mathrm{s}\mathrm{h}\mathrm{e}\mathrm{r} $ $ \mathrm{S}\mathrm{U}\mathrm{P}\mathrm{r} $ 86.2500 ***
(0.0000 )− 5.4245 ***
(0.0000 )86.2500 ***
(0.0000 )平稳 $ \mathrm{N}\mathrm{U}\mathrm{r} $ 65.3799 ***
(0.0000 )− 4.0319 ***
(0.0000 )65.3799 ***
(0.0000 )平稳 $ \mathrm{C}\mathrm{P}\mathrm{r} $ 66.3441 ***
(0.0000 )− 4.4017 ***
(0.0000 )66.3441 ***
(0.0000 )平稳 表 4 最优滞后项的确定
滞后阶数$ \mathrm{l}\mathrm{a}\mathrm{g} $ $ \mathrm{B}\mathrm{I}\mathrm{C} $ $ \mathrm{A}\mathrm{I}\mathrm{C} $ $ \mathrm{Q}\mathrm{I}\mathrm{C} $ 1 − 45.3127 *40.29036 5.570183 *2 − 18.25888 38.80983 15.66304 3 − 7.398458 21.1359 *9.562505 注:带*的数据所对应的是最优滞后阶数。 表 5 格兰杰因果检验表
原假设(前一序列不是后一序列
的格兰杰原因)$ {Ch}^{2} $ $ \mathrm{d}\mathrm{f} $ 是否拒绝
原假设$ \mathrm{N}\mathrm{U}\mathrm{r}-\mathrm{S}\mathrm{U}\mathrm{P}\mathrm{r} $ 18.269 1 是*** $ \mathrm{C}\mathrm{P}\mathrm{r}-\mathrm{S}\mathrm{U}\mathrm{P}\mathrm{r} $ 18.730 1 是*** $ \mathrm{N}\mathrm{U}\mathrm{r}\mathrm{和}\mathrm{C}\mathrm{P}\mathrm{r}-\mathrm{S}\mathrm{U}\mathrm{P}\mathrm{r} $ 20.632 2 是*** $ \mathrm{S}\mathrm{U}\mathrm{P}\mathrm{r}-\mathrm{N}\mathrm{U}\mathrm{r} $ 19.209 1 是*** $ \mathrm{C}\mathrm{P}\mathrm{r}-\mathrm{N}\mathrm{U}\mathrm{r} $ 8.173 1 是*** $ \mathrm{S}\mathrm{U}\mathrm{P}\mathrm{r}\mathrm{和}\mathrm{C}\mathrm{P}\mathrm{r}-\mathrm{N}\mathrm{U}\mathrm{r} $ 26.489 2 是*** $ \mathrm{S}\mathrm{U}\mathrm{P}\mathrm{r}-\mathrm{C}\mathrm{P}\mathrm{r} $ 19.712 1 是*** $ \mathrm{N}\mathrm{U}\mathrm{r}-\mathrm{C}\mathrm{P}\mathrm{r} $ 10.340 1 是*** $ \mathrm{S}\mathrm{U}\mathrm{P}\mathrm{r}\mathrm{和}\mathrm{N}\mathrm{U}\mathrm{r}-\mathrm{C}\mathrm{P}\mathrm{r} $ 60.103 2 是*** 表 6
$ \mathrm{G}\mathrm{M}\mathrm{M} $ 估计结果$ \mathrm{S}\mathrm{U}\mathrm{P}\mathrm{r} $ $ \mathrm{N}\mathrm{U}\mathrm{r} $ $ \mathrm{C}\mathrm{P}\mathrm{r} $ 滞后一期的$ \mathrm{S}\mathrm{U}\mathrm{P}\mathrm{r} $ 0.527562 ***
(4.62)0.4348363 ***
(3.96)0.7717781 ***
(4.23)滞后一期的$ \mathrm{N}\mathrm{U}\mathrm{r} $ 0.6514911 ***
(3.78)0.6539842 ***
(4.98)0.8152604 ***
(4.64)滞后一期的$ \mathrm{C}\mathrm{P}\mathrm{r} $ − 0.1347383 ***
(−4.42)− 0.2698053 ***
(−4.53)− 0.4532845 ***
(−5.39) -
[1] 中国共产党第十九届中央委员会第五次全体会议公报[EB/OL]. (2020-10-29)[2022-09-05]. https://www.gov.cn/xinwen/2020-10/29/content_5555877.htm. [2] 黄勤, 曹汐. 产业结构升级在新型城镇化进程中的作用[J]. 城市问题,2016(7):64-68. [3] 刘淑茹, 段勇恒, 党继强. 产业结构优化、城乡收入差距与城镇化高质量发展[J]. 生产力研究,2021(8):61-65. doi: 10.3969/j.issn.1004-2768.2021.08.012 [4] 刘婷. 株洲新型城镇化对产业结构升级的影响[J]. 管理观察,2015(21):31-33. doi: 10.3969/j.issn.1674-2877.2015.21.009 [5] 陈思宇. 江苏城镇化与产业结构升级互动发展研究[D]. 南京: 中共江苏省委党校, 2015. [6] 熊兴, 余兴厚, 汪亚美. 成渝地区双城经济圈新型城镇化与产业结构升级互动关系研究[J]. 经济体制改革,2022(2):42-49. [7] 王旭. 在产业结构升级中大力推进共同富裕[J]. 资源与人居环境,2022(4):58-59. doi: 10.3969/j.issn.1672-822X.2022.04.016 [8] 吴宇轩, 谢瀚洋, 江俊佑. 产业发展、城乡收入差距及其区域差异性: 基于2005—2019年省际面板数据[J]. 现代商贸工业,2021,42(34):13-16. [9] 周国富, 陈菡彬. 产业结构升级对城乡收入差距的门槛效应分析[J]. 统计研究,2021,38(2):15-28. [10] 李欣. 产业结构升级与新型城镇化良性互动的机理与实证研究[D]. 长沙: 湖南师范大学, 2015. [11] 孙学涛, 于婷, 于法稳. 新型城镇化对共同富裕的影响及其作用机制: 基于中国281个城市的分析[J]. 广东财经大学学报,2022,37(2):71-87. doi: 10.3969/j.issn.1008-2506.2022.2.gdsxyxb202202007 [12] 徐仙英, 张雪玲. 中国产业结构优化升级评价指标体系构建及测度[J]. 生产力研究,2016(8):47-51. [13] 刘建江, 易香园, 王莹. 新时代的产业结构升级: 内涵、困难及推进思路[J]. 湖南社会科学,2021(5):67-76. [14] 李伟军, 王春阳. 金融集聚对新型城镇化影响的门槛效应[J]. 安徽工业大学学报(社会科学版),2018,35(4):9-12. [15] 《中共中央国务院关于支持浙江高质量发展建设共同富裕示范区的意见》发布[J]. 中国注册会计师, 2021(7): 6. [16] 陈丽君, 郁建兴, 徐铱娜. 共同富裕指数模型的构建[J]. 治理研究,2021,37(4):5-16. doi: 10.3969/j.issn.1007-9092.2021.04.002 [17] 伍格. 新型城镇化与产业结构升级[D]. 南昌: 江西财经大学, 2021. [18] 胡元瑞, 田成志, 吕萍. 产业结构升级与新型城镇化建设的时空耦合效应机理与实证研究[J]. 工业技术经济,2020,39(9):80-87. doi: 10.3969/j.issn.1004-910X.2020.09.010 [19] 李盼道. 产业结构与新型城镇化协同关系研究: 以北京市朝阳区为例[J]. 电子科技大学学报(社科版),2018,20(2):68-78.



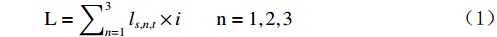
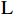
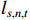
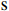
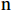
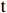
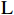
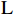

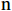
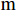
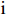
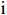
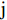
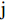
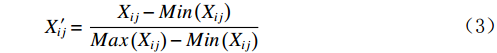
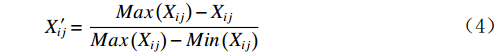
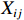
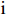
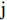
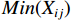
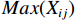
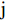
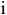
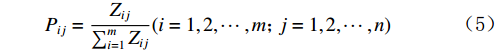
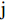
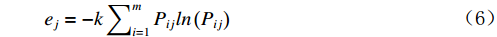
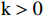
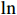
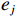
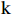
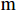
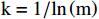
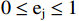
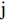


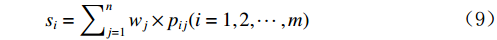
 下载:
下载: